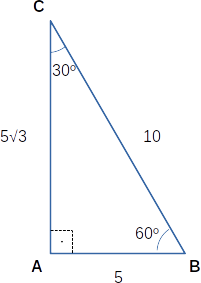
Seja T o triângulo ABC com lados de tamanho 10, 5 e 5√3 , com a relação entre seus ângulos BAC > BCA > ABC. Dada a circunferência C inscrita no triângulo ABC interceptando-o nos pontos P ∈ BC, Q ∈ AC e R ∈ AB.
Qual é o perímetro do quadrilátero convexo PBRQ?
- 5/2(5 − √2 + √3 + √6)
- 5/3(1 − √2 + √3 - √6)
- 1/2(5 + √2 - √3 + √6)
- 5/2(5 − √2 + √3 - √6)
- 1/3(1 − √2 + √3 + √6)
Resolução
Usando o teorema de pitágoras, verifica-se q o triângulo ABC é retângulo em A:
√(5² + 5².3) = √10²
Usando relações trigonométricas podemos obter os ângulos B e C:
cos B = AB/BC
cos B = 5/10 = 1/2
B = 60º
sen C = AB/BC
sen C = 5/10 = 1/2
C = 30º
Os segmentos tangentes com ponto comum são congruentes:
BP = BR
AR = AQ
CQ = CP
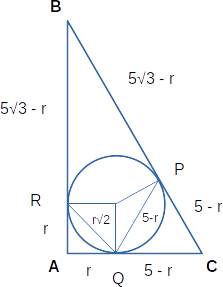
No triângulo AQR podemos usar pitágoras pra encontrar a hipotenusa. Daí, RQ = r√2.
Note q o triângulo CPQ é equilátero. Daí, PQ = 5-r.
A fórmula do raio da circunferência inscrita num triângulo retângulo é:
r = (a + b - c)/2
Então:
r = (5 + 5√3 - 10)/2
r = 5(√3 - 1)/2
Finalmente, o perímetro de PBRQ é:
2p = 2.(5√3 - r) + r√2 + 5-r
2p = 10√3 - 3r + r√2 + 5
2p = 5 + 10√3 + r(√2 - 3)
2p = 5 + 10√3 + 5(√3 - 1)/2 . (√2 - 3)
2p = 5 + 10√3 + 5(√6 - 3√3 - √2 + 3)/2
2p = (10 + 20√3 + 5√6 - 15√3 - 5√2 + 15)/2
2p = (25 + 5√3 + 5√6 - 5√2)/2
2p = 5(5 - √2 + √3 + √6)/2
Gabarito: (A)
