Um reservatório cônico está sendo cheio a uma vazão de 2 m³/s. O reservatório possui 9 metros de altura e sua base possui 6 metros de diâmetro. O quão rápido o nível da água está subindo quando a água estiver a 6 metros do topo?
- 3/8π m/s
- 1/2π m/s
- 4/π m/s
- 9/8π m/s
- 2/π m/s
Resolução
O enunciado não deixa explícito a orientação do cone (ie: de pé ou
invertido), o q abre margem pra interpretações. Então vamos fazer as
duas contas e comparar com as múltiplas escolhas disponíveis.
Hipótese 1: Cone de Pé
Segue um corte longitudinal do cone:
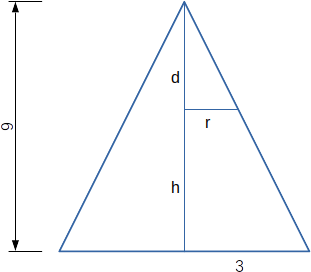
Por semelhança de triângulos é observa-se que:
r/d = 3/9
Então:
r = d/3
Observa-se tb q:
d + h = 9
O volume da região preenchida de água é:
V = π.3².9/3 - π.r².d/3
V = 27π - π.d³/27
V = 27π - π.(9-h)³/27
Derivando esse volume obtemos:
dV/dt = 3π.(9-h)²/27 . dh/dt
2 = π(9-h)²/9 . dh/dt
Para h=3 temos:
2 = π(9-3)²/9 . dh/dt
2 = 36π/9 . dh/dt
2 = 4π . dh/dt
dh/dt = 1/2π
Gabarito: (B)
Hipótese 2: Cone Invertido
Segue um corte longitudinal do cone:
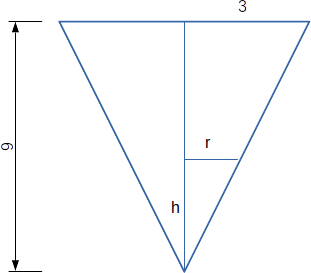
Por semelhança de triângulos é observa-se que:
r/h = 3/9
Então:
r = h/3
O volume da região preenchida de água é:
V = πr².h/3
V = πh³/27
Derivando esse volume obtemos:
dV/dt = 3πh²/27 . dh/dt
2 = πh²/9 . dh/dt
Para h=3 temos:
2 = π3²/9 . dh/dt
2 = π . dh/dt
dh/dt = 2/π
Resposta: (E) ?!?!?!?!
hummm … isso é um problema! Se considerarmos q o cone está invertido
(ex: um reservatório subterrâneo), ainda assim haveria uma opção com a
resposta desse caso.
IMHO, a banca deveria aceitar as duas respostas.
