O Batalhão de Comando e Serviços da ESA é composto por 𝑛 homens e 𝑚 mulheres e foi acionado para uma operação no centro da cidade de Três Corações – MG. O Comandante do Batalhão deve formar um grupamento com 𝑟 militares, 𝑟 ≤ 𝑛 e 𝑟 ≤ 𝑚. Assim, o número de grupamentos que podem ser formados é dado por:
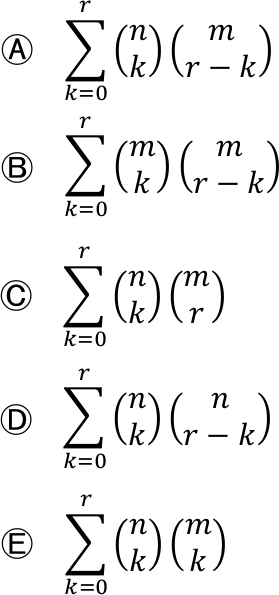
Resolução
Precisamos tomar k homens dentre os n homens disponíveis. Daí tem-se o seguinte número de combinações:
Cn,k = n! / k!(n-k)!
Posteriormente precisamos tomar (r-k) mulheres dentre as m mulheres disponíveis. Daí tem-se o seguinte número de combinações:
Cm,r-k = m! / (r-k)!(m-r+k)!
Podemos usar o teorema fundamental de contagem (ie: regra do produto) para obter o número total de combinações desses dois casos para um caso específico de k:
ak = Cn,k.Cm,r-k
Como k pode ser qq valor entre 0 ≤ k ≤ r, então devemos fazer o somatório de todos esses casos:
N = ∑rk=0 ak
N = ∑rk=0 Cn,k.Cm,r-k
Gabarito: (A)
