Prova Modelo D
Questão 18
A quantidade de números inteiros que satisfazem a inequação √x-1 / (x²-4x) ≤ 0 é igual a:
[A] 1
[B] 2
[C] 3
[D] 4
[E] 5
Resolução
Inicialmente vamos declarar as seguintes funções:
f(x) = √x-1
g(x) = x²-4x
Para f(x) temos o seguinte comportamento do sinal:
x > 1 => f(x) > 0
x = 1 => f(x) = 0
x < 1 => f(x) ∉ ℝ
Para g(x), note q podemos reescrever da seguinte forma fatorada:
g(x) = x²-4x = x.(x-4)
Logo o comportamento de seu sinal é:
x > 4 => g(x) > 0
x = 4 => g(x) = 0
0 < x < 4 => g(x) < 0
x = 0 => g(x) = 0
x < 0 => g(x) > 0
Para f(x)/g(x) teremos o seguinte comportamento do sinal:
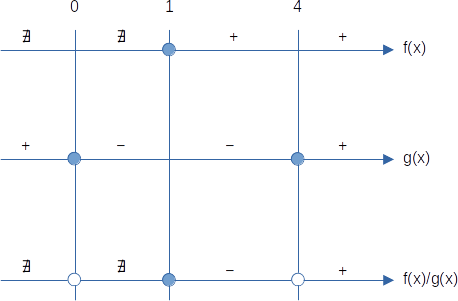
Ou seja, f(x)/g(x) ≤ 0 apenas para 1 ≤ x < 4.
Finalmente, no intervalo [1,4[ existem apenas 3 números
inteiros {1,2,3}.
Gabarito: (C)
