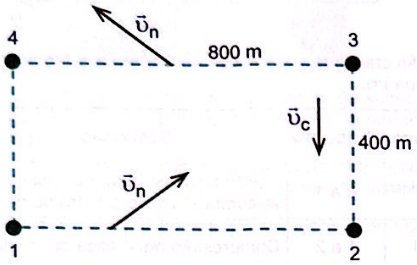
Para os circuitos de maratonas aquáticas realizadas em mares calmos e próximos à praia, é montado um sistema de boias que determinam o trajeto a ser seguido pelos nadadores. Uma das dificuldades desse tipo de circuito é compensar os efeitos da corrente marinha. O diagrama contém o circuito em que deve ser realizada uma volta no sentido anti-horário. As quatro boias estão numeradas de 1 a 4. Existe uma corrente marinha de velocidade vc, cujo módulo é 30 metros por minuto, paralela à praia em toda a área do circuito. Nas arestas mais longas, o nadador precisará nadar na direção apontada pelos vetores vn dos pontos 1 até 2 e de 3 até 4. Considere que a velocidade do nadador é de 50 metros por minuto, em relação à água, durante todo o circuito.
Nessa situação, em quantos minutos o nadador completará a prova?
- 42
- 65
- 72
- 105
- 120
Resolução
Trechos 1-2 e 3-4
Nesses trechos a velocidade do nadador vn será a soma dos seguintes vetores ortogonais:
vn = v + vc
vn² = v² + vc²
v² = vn² − vc²
v² = 50² − 30²
v = 40 m/min
Podemos usar a fórmula de cinemática para obter o tempo necessário para percorrer esses trechos:
t = d/v
t = 800/40
t = 20 min
Ou seja, cada um dos trechos 1-2 e 3-4 levará 20 minutos para ser
percorrido.
Trecho 2-3
v = 50 - 30
v = 20 m/min
O tempo pra percorrer esse trecho será:
t = 400/20
t = 20 min
Trecho 4-1
v = 50 + 30
v = 80 m/min
O tempo pra percorrer esse trecho será:
t = 400/80
t = 5 min
Finalmente, o tempo total de percurso será 20 + 20 + 20 + 5 = 65
minutos.
Resposta: (B)
