EFOMM 2024/2025: Matemática

Calcule o volume do sólido reto com altura h=12 em que sua base é definida, no primeiro quadrante, abaixo dos gráficos das funções g e h e acima do gráfico da função f, onde

f(x) = x² − 8x + 17;
g(x) = x² − 4x + 9; e
h(x) = x² − 12x + 41.

1. 360 u.v.
2. 192 u.v.
3. 144 u.v.
4. 72 u.v.
5. 64 u.v.

Resolução

Primeiramente é preciso visualizar as gráficos das funções quadráticas acima:

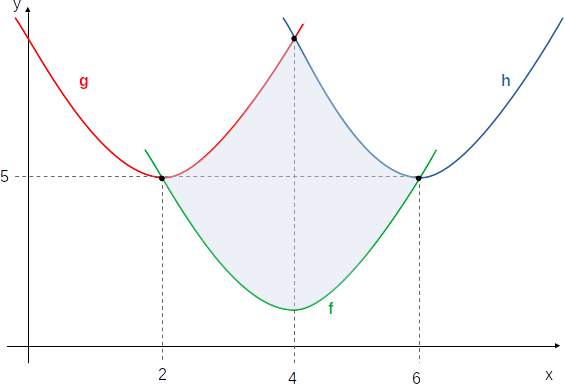
Onde os vértices dessas funções são determinados pela fórmula:

V: (x_v,y_v) = (-b/2a,-Δ/4a)

E os pontos de intersecção são determinados por:

f(x) = g(x)
x² − 8x + 17 = x² − 4x + 9
-8x + 17 = -4x + 9
17 − 9 = 8x − 4x
4x = 8
x = 2

f(x) = h(x)
x² − 8x + 17 = x² − 12x + 41
-8x + 17 = -12x + 41
12x − 8x = 41 − 17
4x = 24
x = 6

g(x) = h(x)
x² − 4x + 9 = x² − 12x + 41
-4x + 9 = -12x + 41
12x − 4x = 41 - 9
8x = 32
x = 4

A área em destaque pode ser calculada por:

S_b = ∫₂⁴ (g(x)-f(x))dx + ∫₄⁶ (h(x)-f(x))dx
S_b = ∫₂⁴ (4x - 8)dx + ∫₄⁶ (-4x + 24)dx
S_b = (2x² - 8x)|₂⁴ + (-2x² + 24x)|₄⁶
S_b = (2.4² - 8.4 - 2.2² + 8.2) + (-2.6² + 24.6 - -2.4² - 24.4)
S_b = (32 - 32 - 8 + 16) + (-72 + 144 + 32 - 96)
S_b = 8 + 8
S_b = 16

O volume do sólido reto será:

V = S_b × h
V = 16 × 12
V = 192

Gabarito: (B)