Uma das atividades previstas para comemorar o aniversário da ESA, foi uma competição de tiro. Essa competição consistia em lançar um alvo móvel e o atirador efetuar um disparo para tentar acertá-lo. Em uma das rodadas, a trajetória do alvo foi dada por 𝑓(𝑡) = −2/9 𝑡² + 4/3 𝑡, em que 𝑡 é o tempo, em segundos, após o disparo. A altura do alvo é representada, em km, por 𝑓(𝑡). Após um segundo, e do mesmo local de onde o alvo foi lançado, o atirador inclinou sua arma 45º, realizou um disparo retilíneo e acertou o alvo. Qual a altura do alvo quando ele foi atingido?
Ⓐ 1,6 km
Ⓑ 1,7 km
Ⓒ 1,8 km
Ⓓ 1,9 km
Ⓔ 2,0 km
Resolução
A posição do alvo em função do tempo pode ser expressa por:
x(t) = v0xt
y(t) = 4t/3 - 2t²/9
A posição do disparo em função do tempo pode ser expressa por:
x’(t) = (v’0/√2).(t-1)
y’(t) = (v’0/√2).(t-1)
Para q o disparo acerte o alvo devemos satisfazer:
x(t) = x’(t)
v0xt = (v’0/√2).(t-1)
y(t) = y’(t)
4t/3 - 2t²/9 = (v’0/√2).(t-1)
Daí:
v0xt = 4t/3 - 2t²/9
hummm … uma equação e duas incógnitas … não tem como
resolver …
Gabarito: (E)
No entanto, essa questão deveria ser é anulada !!!
Resolução Errada: Interpretação Criativa
Considere o gráfico abaixo:
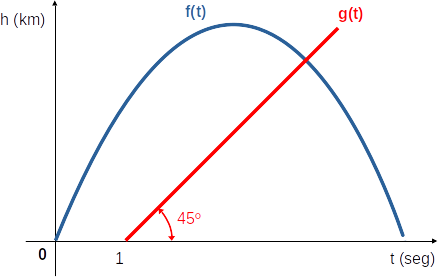
A curva azul corresponde a função f(t) do alvo, analogamente a curva
vermelha corresponde a função g(t) do disparo.
Se assumirmos q o enunciado quis dizer é q a curva vermelha tem 45º, então:
g(t) = t - 1
Daí, no momento do impacto teremos:
f(t) = g(t)
−2t²/9 + 4t/3 = t - 1
-2t² + 12t = 9t - 9
2t² - 3t - 9 = 0
Usando a fórmula de Bhaskara pra essa equação do 2º temos:
Δ = b² - 4ac
Δ = 9 - 4.2.-9
Δ = 81
t = (-b ± √Δ)/2a
t = (3 ± 9)/4
Como t > 0:
t = 3 s
Daí:
f(3) = −2.3²/9 + 4.3/3
f(3) = −2 + 4
f(3) = 2km
Gabarito: (D)
No entanto, pra chegar nesse resultado foi necessário uma interpretação
errada do enunciado.
Portanto, essa questão deveria ser anulada!
