Na figura abaixo, observamos o esboço de dois gráficos 𝑓(𝑥) = 𝑒x e 𝑔(𝑥) = ln(𝑥)
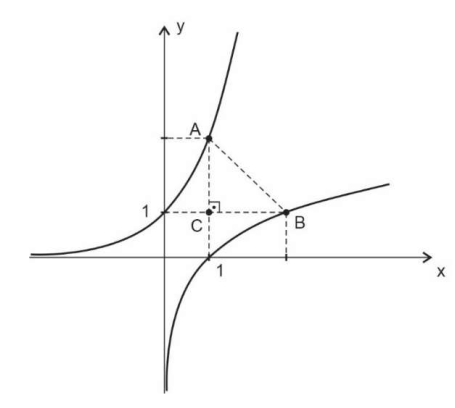
Com base nas curvas e suas respectivas leis de formação, é correto afirmar que o perímetro do triângulo A, B, C em unidades de comprimento, é igual a
- (2 + √2)(𝑒 − 1)
- (2 − √2)(𝑒 + 1)
- (2 + √2)(𝑒 + 1)
- (2 − √2)(𝑒 − 1)
Resolução
Pelo gráfico podemos obter facilmente as coordenadas dos pontos A e C:
A = (1, e)
C = (1, 1)
Para o ponto B note q:
ln(xb) = 1
xb = e
Portanto:
B = (e, 1)
Daí, os catetos AC e BC medem:
AC = C - A
AC = (1, 1) - (1, e)
AC = (0, 1 - e)
|AC| = √( 0² + (1 - e)² )
|AC| = e - 1
BC = C - B
BC = (1, 1) - (e, 1)
BC = (1 - e, 0)
|BC| = √( (1 - e)² + 0² )
|BC| = e - 1
Usando teorema de Pitágoras obtém-se a medida da hipotenusa AB:
|AB| = √2.(e - 1)
Finalmente, o perímetro do triângulo ABC é:
2p = 2(e - 1) + √2.(e - 1)
2p = (2 + √2).(e - 1)
Gabarito: (A)
